Understanding Sag and Tension in Power Lines
Transmission lines are a lifeline of modern electrical systems, and understanding their behavior under various conditions is critical for safe and efficient power delivery. Two essential concepts in transmission line design are sag and tension. These determine how the line behaves under different loads, weather conditions, and spans.
In this guide, we will explore sag and tension and their interdependence.
Why Sag and Tension Matter in Power Lines
Sag-tension calculations are critical for designing and maintaining transmission and distribution lines. They predict the sag and conductor tension under varying conditions, such as temperature changes, ice buildup, and wind loads.
Maximum conductor tension is an important factor in structure design. On the other hand, maximum conductor sag determines structure heights and locations to maintain electrical clearances. Hence, accurate sag-tension calculations are vital in mechanical and electrical integrity of transmission or distribution lines.
Understanding Sag in Electrical Conductors
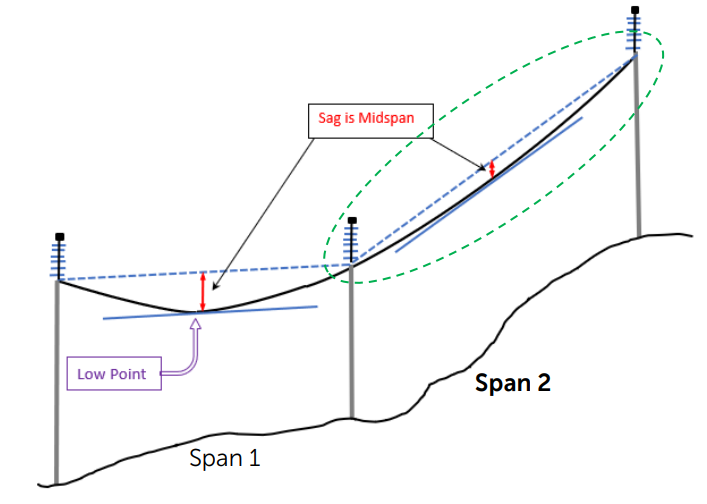
When you search for the definition of “sag”, you’ll often find something like this:
“Sag is the vertical distance between the support and the lowest point of the conductor.”
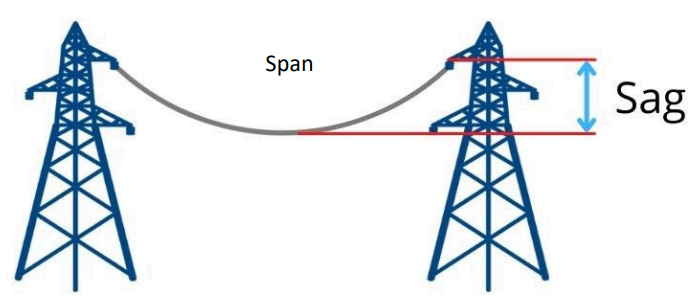
While this is true for level supports, it doesn’t capture the full picture. The National Electrical Safety Code (NESC 2017) provides a more accurate definition:
“The distance measured vertically from a conductor to the straight line joining its two points of support. Unless otherwise stated in the rule, the sag referred to is the sag at the midpoint of the span.”

Why the NESC Definition Matters
The NESC definition is crucial because it accounts for situations where the supports are at different heights (an unlevel span). In these cases, the lowest point of the conductor might not be directly below the midpoint.
Think of it this way:
- Any point along the conductor has a sag – it’s simply the vertical distance between that point and the imaginary straight line connecting the supports.
- Midpoint sag is a specific type of sag and often what’s meant when people simply say “sag.”
- Maximum sag is the greatest sag along the conductor, which may or may not be at the midpoint, especially in unlevel spans.
Clarifying Terminology
To avoid confusion, it’s best to be precise with our language:
- Use “sag” when referring to the general concept.
- Use “midpoint sag” when specifically discussing the sag at the midpoint of the span.
- Use “maximum sag” when referring to the greatest sag along the conductor.
This article will explain these concepts, provide key formulas, and show how to calculate sag and tension for real-world applications.
Understanding Tension in Electrical Conductors
Now, after we understand the sag. Let’s revisit the fundamentals of tension in a conductor.
Vertical Tension Only
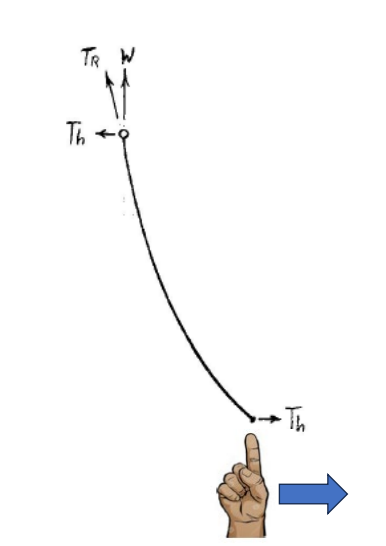
Imagine a simple chain hanging from a single attachment point. What happens here?
To maintain equilibrium at the attachment point, the Tension must be equal to the total Weight of the chain.
As you move down the chain, tension decreases to zero at the lowest point.

Adding Horizontal Tension
Mathematically, the resultant tension is:
What happens when you pull harder?

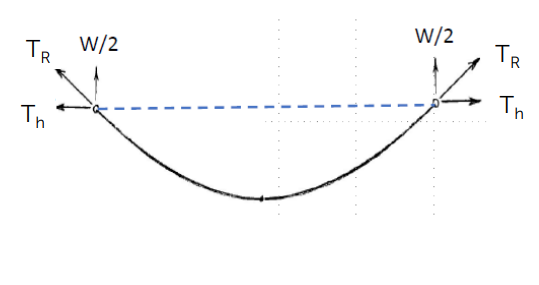
Level Span
When both ends of a chain (or conductor) are fixed at equal heights:
- Half the weight of the chain is supported by each attachment point.
- Tension along the cable varies, being greatest near the supports and least at the lowest point.
Inclined Span
What if one end is higher than the other?
- All the weight of the chain is supported at the higher point if there is no low point.
- If there is a low point, the weight is divided proportionally between the two supports.
In an inclined span, there might be no lowest point of the conductor as shown in the figure. In this case, all the weight of the conductor is supported by the higher support.
Relationship Between Sag and Tension
We understand the basic concepts of sag and tension. Now let’s investigate the relationship between the two. Moving forward, when we mention sag in this article, we are referring to the midpoint sag of a level span.

In a level span, sag is, generally, inversely proportional to the horizontal tension (Th),
- Increase tension, and the sag decreases
- Decrease tension, and the sag increases
Conversely, in a level span, horizontal tension is, generally, inversely proportional to the sag:
- Decrease sag, and the tension increases
- Increase sag, and the tension decreases
Important Notes:
In a level span, at midspan there is no weight acting at that point. This is because the weight is supported at the attachment points. This may not be intuitive, but it is nevertheless true.
Summary
We have discussed the basic concepts of sag and tension and their relationship. But we are just on the tip of the iceberg. The next article will dig dipper on the factors affecting sag and the mathematics behind it.
In an ideal, non-flexing scenario, the conductor would form a straight line between the two supports. However, due to its weight, the actual path of the conductor forms a catenary curve.
References:
- https://incabamerica.com/learning-hub/
- NS220 Overhead Design Manual
- RUS Bulletin 1724E-200
- Overhead Power Line Design – F. Kiessling , P. Nefzger, J.F. Nolasco and U. Kaintzyk
- Principles of Power System – K. Mehta

